The last shot in crokinole, aka the hammer, it’s an advantage right? Certainly! We all know that and it’s perhaps the first bit of strategy any competitive player knows; if it’s all tied up and you’ve got the hammer, you are probably in a position to win.

But how important is it to have the hammer? For a while I’ve thought the advantage of hammer between two equally skilled players was around 60-40. (That is, against an equal opponent the player with hammer would win a single round 60% of the time.) This wasn’t based on any analysis, just a feeling really, and I had a feeling the hammer advantage for doubles play was slightly higher, maybe 65%.

Such an advantage for the hammer, if those percentages were accurate, is significant so it’s a good thing crokinole games are typically four rounds so that such an advantage is nullified. There is of course one exception, which is elimination matches where a tie is not an acceptable result.

A history of elimination formats

Thanks to a 1960 article on the Ontario Crokinole Championships, and to Howard Martin for digging it up, we know the concept of a “first to X points” race format is long familiar to crokinole.

The World Championships utilized a slightly more sophisticated approach, with a best of 3 games format with each game being a race to 5 points. The early years of the NCA saw many innovations for competitive crokinole, but the format used for nearly all championship matches remained identical to that of the World Championships.

Either format was widely considered acceptable for tournament elimination matches, however it was openly acknowledged that both formats presented an inherent advantage for one player. Under the circumstances of closely contested play, the championship match would be determined by one final round that would break a tie, and thus one player would have the hammer advantage for one additional round. But such a case seemed too rare to expend much energy correcting. After all, how likely was it that a first to 11 points match would be tied 10-10, or that a best of 3 games match would be tied 4-4 in the final game?

It turns out, it happens often enough.

The finals of both the 2011 (Ray Beierling winning over Eric Miltenburg) and 2012 London tournaments (Jason Beierling winning over Ray), as well as the 2012 World Championship final (Jon Conrad defeating Justin Slater) would all be decided with a sudden death round after the 3rd and final game was tied 4-4. In all three matches, the player with the hammer advantage was victorious.

No one was disputing the results of the matches, and generally all agreed it was exciting stuff, but people began to ponder if there was a better way. Only two years earlier a first round Wimbledon tennis match had made headlines by lasting 3 days and 11 hours of playtime. The length of the match was due to a rule that equalizes the number of games where each player has the advantage of serving. One of the players in the match, John Isner, has the second-highest percentage of service games won in the history of tennis, doing so 92% of the time. He also had a relatively poor winning percentage in return games, at around 10%, creating a perfect scenario for an extended match.

The Quinte Region Crokinole Club would be the first to come up with an idea to address crokinole’s hammer advantage, creating the Quinte Convention and running it at the 2012 Belleville Challenge, where it would be used immediately. The format was played as a best of 3 games but allowed any game to be tied 4-4. If after 3 games the players were tied with an equal number of games won and tied, then the match would be decided in successive 2-round mini-games. If one player managed a 4-0 or 3-1 win after each player received the hammer advantage for one round, then the match would be over. But if the score was 2-2, then another set of 2 rounds would be played. Both the semifinals of Jon Conrad vs Brian Cook, and Nathan Walsh vs Fred Slater would require 6 rounds of overtime crokinole to be played to determine a winner.

Around the same time Fred Slater came up with a format he dubbed the Wimbledon rule. It allowed the first two games of a best of 3 to be decided by a one-round tie-breaker, but if the final decisive game was tied 4-4, then successive 2-round mini-games would be utilized until a clear winner emerged.

Personally I greatly enjoyed both of these formats when they were introduced. I liked the idea of a thrilling close-fought battle on the crokinole board being stretched out a bit longer than you’d expect, like a thrilling tennis match or NHL overtime playoff game. But mostly I liked the idea of the equality the format brought to both players. If the hammer advantage would give one player a substantial 60-40 edge to win the match, then it made perfect sense to me to utilize a format that negates it.

Marathons

But then we started to see a few matches where the Wimbledon and Quinte Convention formats were used to their fullest, and I became less enthused.

In the 2013 Belleville B division final, Clare Kuepfer and Phil Somers played the equivalent of 5-games of crokinole and roughly 40 minutes to decide the match. At the 2013 Ontario Doubles Championship, Conrad/Snyder played Johnston/Johnston in a first to 10 points match with a Wimbledon tiebreaker. The match was eventually won 18-16, thanks to the foresight of tournament organizer Ray Beierling who declared the match would switch to sudden death at 16-16. The match took over an hour to complete. The B division semifinals of the 2018 Ontario Singles Championship was a WCC rematch with Robert Bonnett and Jon Conrad. The first to 9 points match should have captured the full attention of the audience as the match was tied 8-8, but spectators drifted away from the board as the Wimbledon rounds extended on and on. Eventually Conrad would win by a score of 18-14 after playing the equivalent of two full matches.

Such marathons caused some headaches for tournament organizers, and the Wimbledon and Quinte Conventions eventually faded from use; the last time it was employed was the 2020 Hamilton final.

Even if the format was fairer, I started to wonder if it was really worth the extra time and waning of spectator interest. From my commentator experience, I feel there is great value in simplicity. Tell your viewer the game is first to 9 points and that’s easy to understand. Tell them it’s a best of 3 games where each game is first to 5 points and they’ll probably still understand. Tell them it’s best of 3 games where each is first to 5, but they stop if it’s 4-4, and then if after all 3 games they are tied because they tied each game, or each won one game and tied the other then they have to keep playing until . . .

You get the point. Not super simple to explain.

And in the simplicity also comes the excitement. Tell the viewer it’s one game, one round, one goal to win the championship, and everyone immediately understands the importance of it. Sports fans love the idea of Game 7 in the playoffs, or sudden death overtime. That really only leaves one question.

Is the excitement worth the inequity?

Even if the advantage of the hammer in a round is worth a 20% edge (60% vs 40%), that does not mean that the player with the hammer has a 20% better chance to the win when the match starts.

If the strength of the hammer is actually 60%, then a race to 9 points format gives the player with potentially one extra hammer a winning chance of 53% against an equally skilled opponent. A 6% edge.

When you extend the match format to something longer, such as the WCC format, the hammer advantage shrinks to about 51.5% vs 48.5% (a 3% edge). Even from a player perspective, such an edge seems negligible in my mind. And from an entertainment perspective, the advantage didn’t seem worth negating at the cost of the sudden death round excitement.

What’s the real hammer strength?

The crokinolereference database has the round-by-round scores from over 5,000 games, and it has information on which player/team had the hammer for 3,000 of those games.

From that data, the advantage of the hammer for one round is 55-45 for singles, and 52-48 for doubles.

(For all images below, clicking of them will access a pdf of higher resolution.)

I found this a little surprising, as the advantage comes in less than I thought it would be for singles, and the doubles result shows the hammer is even less important than in singles (although the sample size is much smaller, and thus the conclusion is less credible).

A 55-45 hammer advantage further shrinks the pre-match advantage in a race to 9 points down to 51.3%-48.7%, and in the WCC format down to 50.6%-49.4%.

I began to wonder if the result would be different if the two players matched up were of equal skill, or if one player was dominant over another. The thought occurred to me that if one player was much stronger than another, then maybe the hammer wouldn’t be an advantage at all since the stronger player may just win every round regardless. Perhaps the existence of these games was skewing the data to show the hammer being less important than it was when two players were of equal skill.

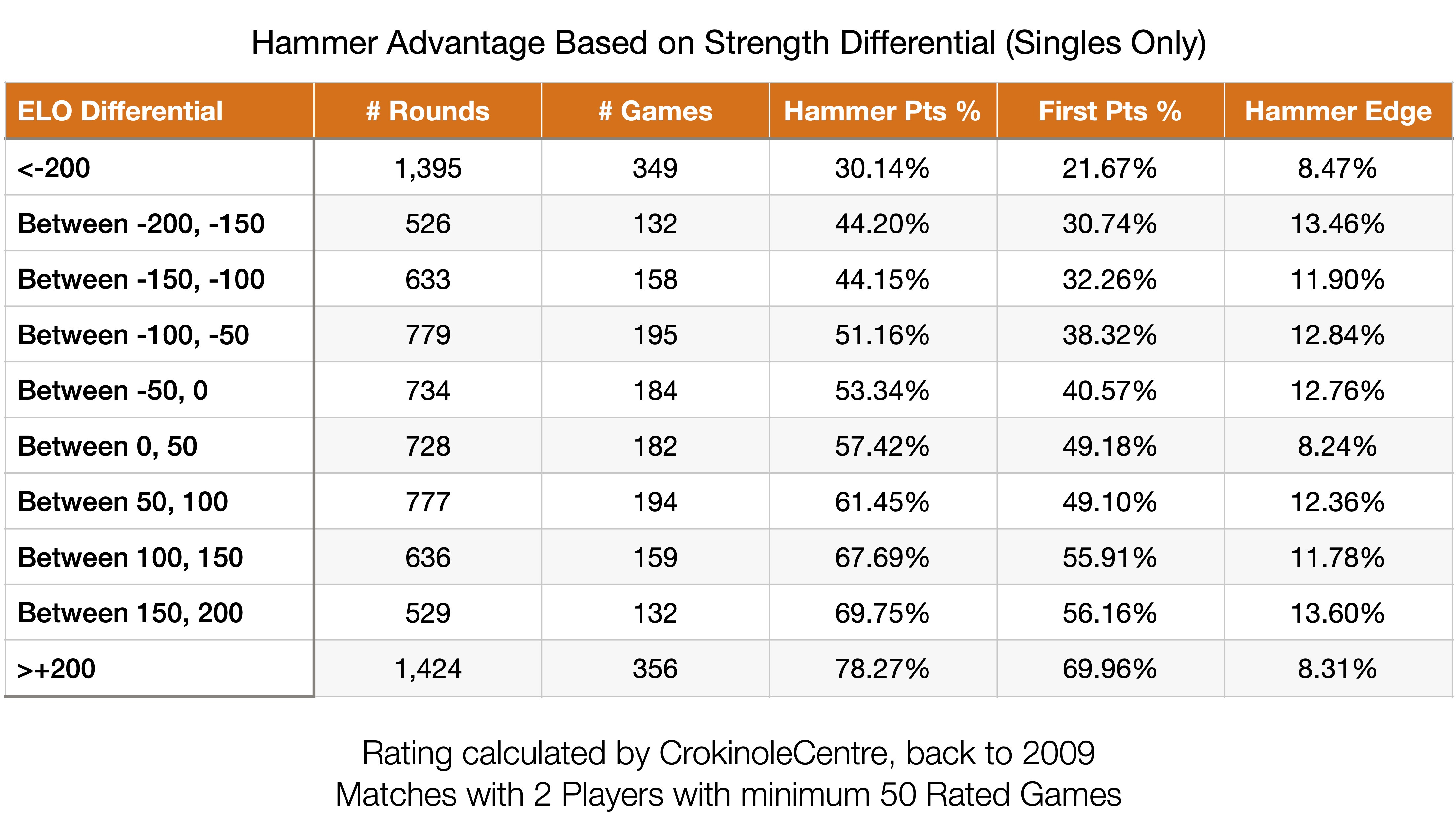
To test this I utilized the ELO ratings I’ve published on crokinolereference, and pulled out the difference in ELO ratings for each game. This reduced the sample size to only singles matches of roughly 2,000 games. I then put all the results into buckets. The first being cases when one player has an ELO rating 200 points below their opponent, the next when the ELO rating is between 150 and 200 points below their opponent, etc.

As you can see, the percentage points scored, both when a player shoots first and when a player has the hammer, increases as their ELO rating is more favourable compared to their opponent. Obviously this makes sense, and at least shows the ELO rating can be used to predict match results.

What is surprising is that the hammer edge remains pretty level regardless of the skill gap between players. Even between matches of equally skilled players, and matches with one dominant player, the advantage of the hammer compared to the disadvantage of shooting first is roughly the same.

A couple of recent Tracey Boards' social media posts also looked at the advantage of the hammer. Analyzing the games from the 2023 WCC revealed it was the case that actually less rounds were won with the hammer.

It got me wondering if there were any tournaments in the database that bucked the 10% hammer edge trend.

There are a couple of tournaments that show hammer advantages much less or more than 10%. However the sample sizes for these events isn’t too substantial.

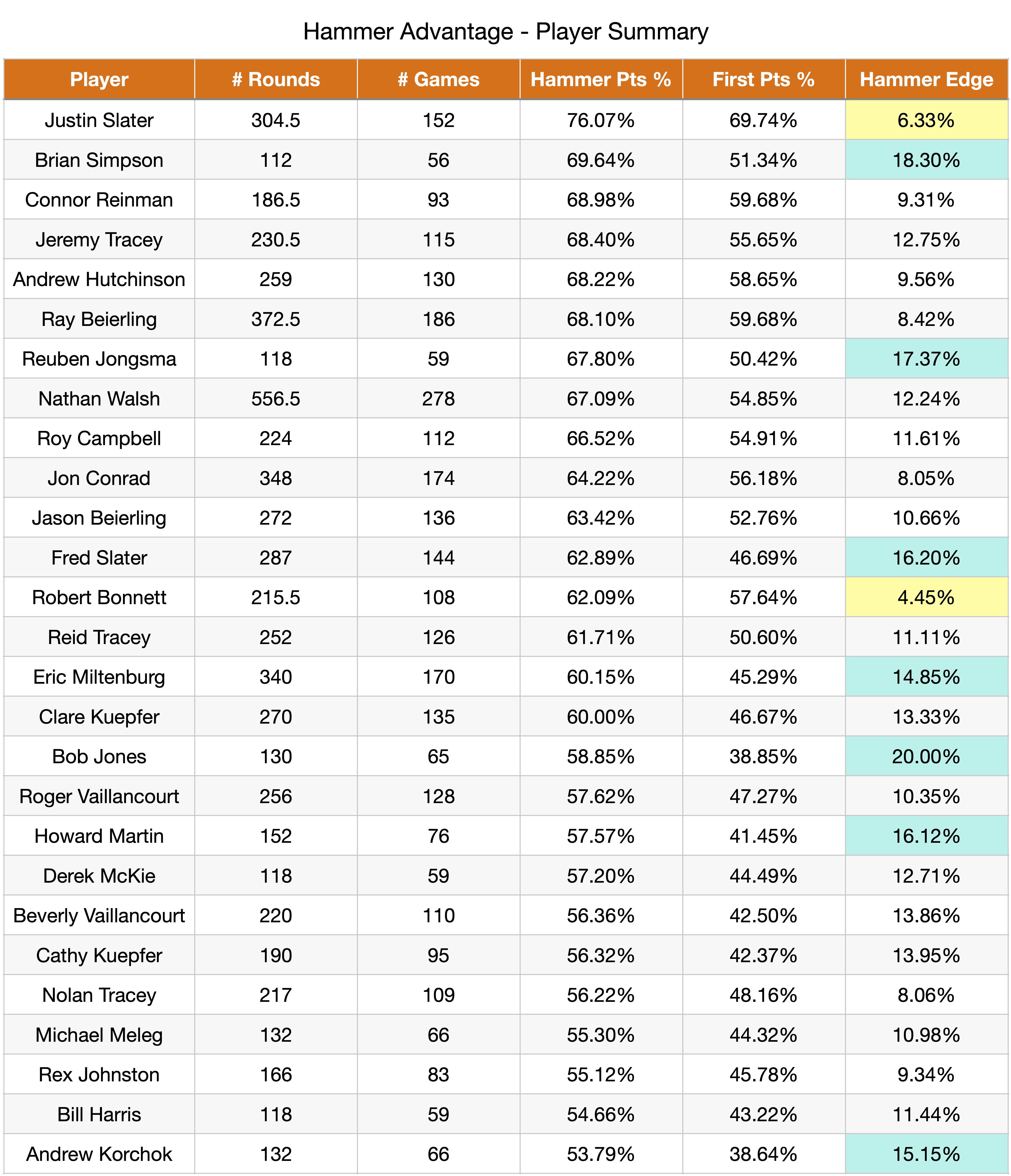
As one last piece of analysis I pulled out the results for a select collection of players, curious to see if there was any players who might be more or less favoured with the hammer. I’ve highlighted some of the highs and lows below.

There are a few players who on either end of the high/low spectrum, but there’s no one who’s drastically far away from the average 10% hammer advantage.

Where does the hammer advantage come from?

The Tracey Boards' post later pointed to the opening round 20 race being a bigger component of which player would win the round. They also found that the player with the hammer more frequently wins the 20 race, which is logical since the player shooting first is more likely to miss first simply because they are the first to shoot.

I decided to dust off some undergraduate math knowledge and calculate the percentage chance of winning the 20 race under varying open 20 proficiency of two players.

The below chart shows the percentage chance that the player with the hammer wins the 20 race, in cases when the player shooting first scores open 20s at the percentages shown in the rows, and the player with the hammer scores open 20s at the percentages shown in the columns.

These probabilities are calculated by conditioning on two geometric probability distributions and assuming the round consists of 8 discs.

The cells where the two players have equal proficiency are highlighted, and shows the hammer’s chance of winning the 20 race is at least 57%, with the advantage improving as the 20 proficiency decreases or increases from 80% success.

I had actually calculated this chart about 10 years ago, and it was the basis for my reasoning thinking the hammer had a 60-40 advantage. It seems to me that players are scoring open 20s with success between 60% and 80%, so I figured the hammer is probably winning the 20 race and the round about 60% of the time. With a similar line of thinking I thought the hammer advantage in doubles would be even higher because it seems to me that open 20% success decreases in that discipline.

Of course there’s more to crokinole than just winning the 20 race.